Applying the Dispersion-Threshold Identification (I-DT) algorithm to identify eye fixations
Oct 27
7 min read
Overview
The I-DT algorithm, alongside the Velocity-Threshold Identification (I-VT) algorithm, is a commonly used eye movement detection algorithm to identify eye fixations. To identify eye fixations, the algorithm relies on the fact that eye fixations, as described by Salvucci and Goldberg, tend to be closely clustered together. As a result, consecutive gazes that occur in close proximity to each other, defined using a dispersion threshold, are grouped together as an eye fixation. In addition, a minimum eye fixation duration threshold is often used when implementing the I-DT algorithm to remove eye fixations that are too short and might have little meaning.
In this blog post, we'll go over the steps needed to apply the I-DT algorithm alongside some sample Python code. Lastly, we'll discuss some key points that you ought to keep in mind when applying the I-DT algorithm to identify eye fixations.
Applying the I-DT algorithm
Salvucci and Goldberg describe that the steps of the I-DT algorithm to be (roughly) the following:
Initialize a window of gaze points that covers the minimum eye fixation duration threshold.
Check whether the window of gaze points meets the dispersion threshold. If so, skip the gaze first point and go back to step 1. Otherwise, go to step 3 below.
Add additional gaze points to the window until the dispersion among the gaze points is above the dispersion threshold.
Define the eye fixation at the centroid of all the window gaze points.
We'll expand upon each of these points further below. In addition, note that the data used in this blog post is the same as the one used in this prior blog post. Feel free to check it out first in order to get a sense of what the data looks like.
Step 1. Initialize a window of gaze points that covers the minimum eye fixation duration threshold.
First, we need define the minimum eye fixation duration threshold that the window of gaze points needs to cover. A commonly used threshold value is 100 ms (i.e. 0.1 seconds), which we'll use for our implementation. Note also that a different minimum eye fixation duration threshold could be selected, something we discuss later in the key points section.
Afterwards, we can iteratively add gaze points until we satisfy the minimum eye fixation duration threshold, as can be observed below:
In this code snippet, we first want to define indexes that we'll iterate over. The first index, current_index, describes where we currently are in the data. The second index, final index, describes the index at which our gaze point window ends. Lastly, the max_index, represents the length of our overall data (i.e. how many gaze points there are).
Then, the entire I-DT algorithm is contained within a While loop that we use to continue iterating over the gaze points until we reach the end (end condition not visible in this snippet -- it'll be shown later). While we're in the loop, we first want to iterate over the gaze points via Python's range function. More specifically, we use the indexes to grab increasingly large slices of data that we save to the variable data_slices.
We check the duration of the gaze points in the data slice, which we can calculate by subtracting the timestamp of the last gaze from the first gaze. If the duration is met, we break out of the range's loop, increase the final index, and set a flag that indicates we met the duration threshold. Otherwise, we remain in the range loop, which leads us to grab a data slice with an additional point and check once again whether the duration was met. We also set the flag that indicates whether we met the duration threshold to false.
Step 2. Check whether the window of gaze points meets the dispersion threshold.
Now that we have a group of gaze points that have met the minimum eye fixation duration threshold, we can calculate the dispersion among them. It's important to note that, as Salvucci and Goldberg mention, there are multiple different ways that one can define and calculate the dispersion among gaze points. For instance, Blignaut implemented the I-DT algorithm using 5 different definitions of dispersion used by various eye tracking researchers.
In the present work, to define the dispersion among gaze points, we apply the Distance Dispersion Algorithm. In this approach, the distance (i.e. dispersion) among all the gaze points contained within an eye fixation must be less than a dispersion threshold. In the present work, we set the dispersion threshold as 1 degrees of visual angle.
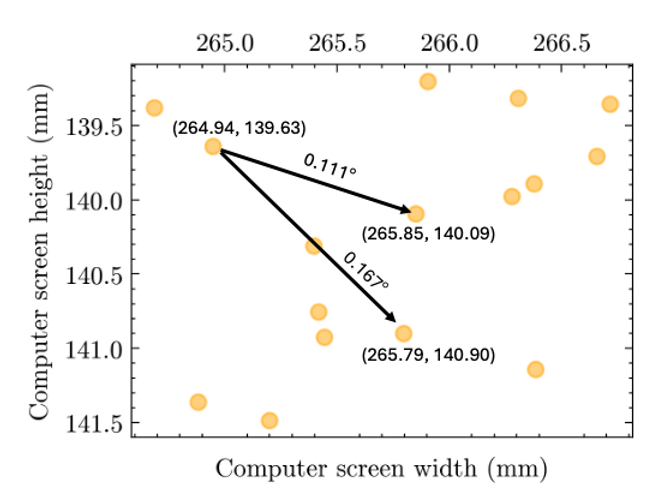
To visualize the dispersion calculation, consider the following example showcasing 16 gaze points. We calculate the dispersion between two gaze points by computing the visual angle between them, as discussed in a previous post. For instance, the angle between the gaze point (264.94, 139.63) (in millimeters) and the gaze point (265.85, 140.09) is 0.111 degrees of visual angle. This process is then repeated from each gaze point to every other gaze point to determine whether the dispersion threshold is ever met.

The code snippet used to apply the Distance Dispersion Algorithm can be observed below. First, we define the algorithm as a function prior to applying it, where we simply iterate over the gaze points twice in order to calculate the dispersion between each point to every other point. During this process, we keep track of each distance and then simply return whichever distance was the largest.
We also define a function to calculate the visual angle between gaze points. To better understand this calculation, you should check out the blog post covering visual angle calculations.
With the functions defined, we can now include the Distance Dispersion Algorithm into our implementation of the I-DT algorithm. We apply the algorithm to determine the current dispersion (i.e. current_dispersion_threshold variable). Afterwards, we check whether we're under the threshold or above it -- which takes our to the next step.
Step 3. Add additional gaze points to the window until the dispersion among the gaze points is above the dispersion threshold.
If our current group of gaze points are below the dispersion threshold, we then continuously add additional gaze points to the group until we meet the dispersion threshold. More specifically:
If the current group of gaze points are above the dispersion threshold, then, as shown in the last code snippet in Step 2, we simply increase the current index by 1 and iterate over the algorithm once again.
Step 4. Define the eye fixation at the centroid of all the window gaze points.
Now that we have a group of gaze points that have both met the minimum eye fixation duration, as well as the dispersion threshold, we're ready to define the eye fixation they represent. To do so, we'll pass the group of gaze points to a function to determine: (1) the duration of the eye fixation; (2) its timetamp; (3) the centroid of the eye fixation.
For example, considering the eye fixation defined for the 16 gaze points we discussed earlier. The location of the eye fixation (blue point) would be positioned right in the middle of all the gaze points (i.e. the centroid).

We call the function in the code after which we've added the additional points to the group of gaze points. You may notice in the code snippet below that we reduce the count of the final index by 1, and slice the fixation data again. The reason we do this, as highlighted by Blignaut, is that we do not want to include the final gaze point -- the one that sent us over the dispersion threshold in our eye fixation. Rather, we want to include only the gaze points whose dispersion remained below the threshold.
We then insert the eye fixation into a dictionary we created earlier, before entering the While loop, as it is easy to transform a dictionary into a Pandas DataFrame later. Note also that we set the current index to the final index plus one, so that the next iteration of the I-DT algorithm starts after the current group of gaze points.
Lastly, the end condition of our overall While loop is whether the duration threshold was met at the start. Recall that we set flags, either True or False, as to whether we met the duration threshold. As we increase the counters iterating over the data, by end of the dataframe, we'll have some points remaining that are not sufficient to meet the duration threshold, and thus, are not a valid sample. As a result, we can simply (although there are probably better ways to code this, including the entire code!) check whether the flag is False. If so, transform the eye fixation data into a dataframe as mentioned before and exist the While loop,
Lastly, applying the code to the entire data and visualizing the eye fixations identified (blue points), as well as the gaze points (orange points), gives us the following plot. Note how the eye fixations are identified on top of clusters of gaze points.

Important details to know
Before wrapping up this post, there are a some key details that you need to be aware of when implementing the I-DT algorithm. The choice of threshold values we selected, 0.1 degrees of visual angle for the dispersion threshold and 100 ms for the minimum eye fixation duration threshold, might need to be different for your respective application. I encourage you to visit the work of Shic et al., as well as Komogortsev et al., and Blignaut to learn more about how important it is to set adequate threshold values as well as some ways to identify which threshold values are appropriate. Also important to note that some algorithms, such as Nyström and Holmqvist's algorithm, automatically set thresholds based on the data collected. In addition, there are other pre-processing steps that are commonly taken, such as smoothing out the data, that we did not apply in our basic implementation.
There are many other key details outside the scope of a single blog post, but these are the some major points that come to mind as I write this. I encourage you to check those works I mentioned earlier as a great starting spot to learn more!
Appendix
Complete implementation of the I-DT algorithm